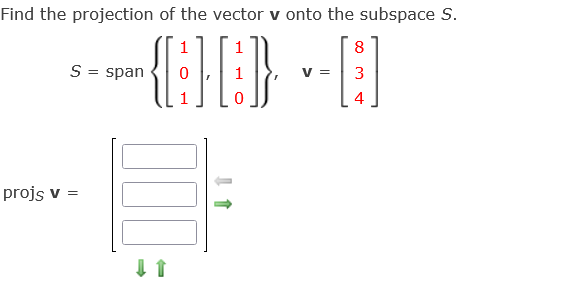
Find the projection of the vector v onto the subspace S.

---

Solution:

For the given subspace S, the vectors u_1 and u_2 are:

u_1=\begin{pmatrix}1\\ 0\\ 1\end{pmatrix},u_2=\begin{pmatrix}1\\ 1\\ 0\end{pmatrix}\\

The vector v is,

v=\begin{pmatrix}8\\ 3\\ 4\end{pmatrix}\\

---

For the vector u_1, the orthogonal vector v_1 is given by,

v_1=u_1\\

v_1=\begin{pmatrix}1\\ 0\\ 1\end{pmatrix}\\

---

For the vector u_2, the orthogonal vector v_2 is given by,

v_2=u_2-\frac{u_1\cdot u_2}{u_1\cdot u_1}u_1\\

v_2=\begin{pmatrix}1\\ 1\\ 0\end{pmatrix}-\frac{\begin{pmatrix}1\\ 0\\ 1\end{pmatrix}\cdot \begin{pmatrix}1\\ 1\\ 0\end{pmatrix}}{\begin{pmatrix}1\\ 0\\ 1\end{pmatrix}\cdot \begin{pmatrix}1\\ 0\\ 1\end{pmatrix}}\begin{pmatrix}1\\ 0\\ 1\end{pmatrix}\\

v_2=\begin{pmatrix}1\\ 1\\ 0\end{pmatrix}-\frac{1+0+0}{1+0+1}\begin{pmatrix}1\\ 0\\ 1\end{pmatrix}\\

v_2=\begin{pmatrix}1\\ 1\\ 0\end{pmatrix}-\frac{1}{2}\begin{pmatrix}1\\ 0\\ 1\end{pmatrix}\\

v_2=\begin{pmatrix}1\\ 1\\ 0\end{pmatrix}-\begin{pmatrix}\frac{1}{2}\\ 0\\ \frac{1}{2}\end{pmatrix}\\

v_2=\begin{pmatrix}\frac{1}{2}\\ 1\\ -\frac{1}{2}\end{pmatrix}\\

---

The projection of the vector v onto the subspace S is given by,

Proj_sv=\frac{v\cdot v_1}{v_1\cdot v_1}v_1+\frac{v\cdot v_2}{v_2\cdot v_2}v_2\\

Proj_sv=\frac{\begin{pmatrix}8\\ 3\\ 4\end{pmatrix}\cdot \begin{pmatrix}1\\ 0\\ 1\end{pmatrix}}{\begin{pmatrix}1\\ 0\\ 1\end{pmatrix}\cdot \begin{pmatrix}1\\ 0\\ 1\end{pmatrix}}\begin{pmatrix}1\\ 0\\ 1\end{pmatrix}+\frac{\begin{pmatrix}8\\ 3\\ 4\end{pmatrix}\cdot \begin{pmatrix}\frac{1}{2}\\ 1\\ -\frac{1}{2}\end{pmatrix}}{\begin{pmatrix}\frac{1}{2}\\ 1\\ -\frac{1}{2}\end{pmatrix}\cdot \begin{pmatrix}\frac{1}{2}\\ 1\\ -\frac{1}{2}\end{pmatrix}}\begin{pmatrix}\frac{1}{2}\\ 1\\ -\frac{1}{2}\end{pmatrix}\\

Proj_sv=\frac{8+0+4}{1+0+1}\begin{pmatrix}1\\ 0\\ 1\end{pmatrix}+\frac{4+3-2}{\frac{1}{4}+1+\frac{1}{4}}\begin{pmatrix}\frac{1}{2}\\ 1\\ -\frac{1}{2}\end{pmatrix}\\

Proj_sv=\frac{12}{2}\begin{pmatrix}1\\ 0\\ 1\end{pmatrix}+\frac{5}{\frac{3}{2}}\begin{pmatrix}\frac{1}{2}\\ 1\\ -\frac{1}{2}\end{pmatrix}\\

Proj_sv=\begin{pmatrix}6\\ 0\\ 6\end{pmatrix}+\begin{pmatrix}\frac{5}{3}\\ \frac{10}{3}\\ -\frac{5}{3}\end{pmatrix}\\

Proj_sv=\begin{pmatrix}\frac{23}{3}\\ \frac{10}{3}\\ \frac{13}{3}\end{pmatrix}\\

---

Final answer:

Proj_sv=\begin{pmatrix}\frac{23}{3}\\ \frac{10}{3}\\ \frac{13}{3}\end{pmatrix}