Types of numbers

Introduction:

Numbers are the fundamental building blocks of mathematics and play a crucial role both in theoretical applications and practical real-life scenarios. In mathematics, numbers are used extensively to quantify, measure, and describe various phenomena. In real life, numbers are ubiquitous and essential in numerous aspects of daily activities. Numbers find application in diverse fields including science, engineering, finance, and economics, where they are utilized for tasks like counting, measurement, and representing quantities. They enable us to make accurate calculations, predictions, and comparisons, facilitating problem-solving and decision-making processes. In conclusion, numbers are indispensable tools in mathematics and real life, serving as the foundation for understanding, analyzing, and interacting with the world.

There are many types of numbers in mathematics, some of the main types of numbers are as follows:

1) Natural numbers (N):

These are the counting numbers starting from 1.

The natural numbers are: {1, 2, 3, 4,…}

2) Whole Numbers (W):

The whole numbers are similar to the natural numbers, the only difference is, that they include zero.

The Whole numbers are: {0, 1, 2, 3, 4,…}

3) Integers (Z):

These include both positive and negative whole numbers and also 0.

The Integers are: {…-3, -2, -1, 0, 1, 2, 3,…}

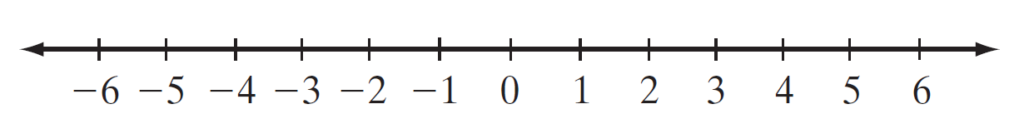
NOTE: The set Z^+ denotes the integers greater than 0.

4) Rational Numbers (Q):

We can write these numbers as fractions. Here both the numerator and the denominator must be integers but, the denominator cannot be zero.

Example: \frac{1}{2},\:\:\frac{3}{4},\:2,\:0, etc.

The Rational numbers can also be terminating (ex. 0.5 or 3.75) or repeating decimals (ex. 0.333… or 0.454545…).

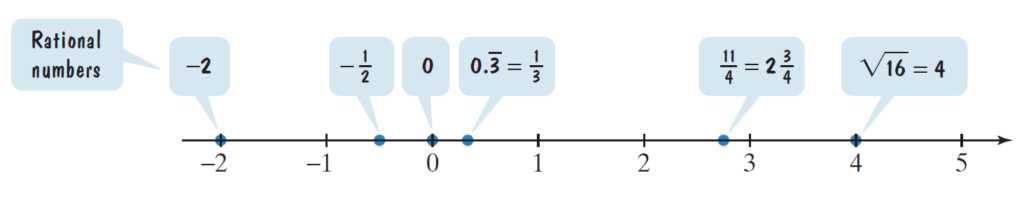
5) Irrational Numbers (R\Q) :

The Irrational numbers cannot be expressed as fractions of integers.

These are non-repeating and non-terminating decimal numbers.

Example: \pi ,\:-\sqrt{5},\:\sqrt{2}, etc.

6) Real Numbers (R):

Real numbers can be both rational and irrational numbers.

Example: -3,\:2,\:1,\:\pi ,\:-\sqrt{5},\:\sqrt{2},\:0, etc.

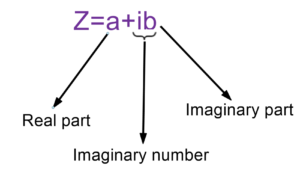
7) Complex Numbers (C):

The complex number is in the form z=a+bi.

Where a and b are real numbers and i^2=-1 or we can say i=\sqrt{-1}

For the number z=a+bi,

‘a’ is called the real part and ‘b’ is called the imaginary part.

Real part denotation: Re(z)

Imaginary part denotation: Im(z)

Example: 1+2i, \:9+8i, \:10+\sqrt{2}i, etc.

Let’s consider one example.

x^2=-1 \\
As we know the square of any real number cannot be negative.

So the solution of the above equation will be a complex solution.

x^2=-1\\
Take a square root on both sides.

x=\pm \sqrt{-1} \\
x=\pm i

The equation has two solutions:

First solution: x=-i

Second solution: x=i

8) Imaginary Numbers Im(z):

When the real part of the complex number is zero then the number is considered an imaginary number.

Example: i, -i, 6i, -7i, etc.

9) Prime number:

If a number is only divisible by 1 and a number itself, then it is called a Prime number.

The prime number is always greater than 1.

NOTE: 1 is not a Prime number.

Example: 2, 3, 5, 7, 11, etc.

10) Composite number:

The natural number which is not a prime number is called a composite number.

Example: 4, 6, 8, 9, 10, 12, etc.

NOTE: 1 is not a Composite number.

NOTE: A composite number is always divisible by 1, a number itself and some other number.

Additionally, there are numeral systems based on different bases, such as:

Binary Numbers: Base-2 numeral system, using only 0 and 1.

Ternary Numeral System: Base-3 numeral system.

Quaternary Numeral System: Base-4 numeral system.

Octal: Base-8 numeral system.

Decimal: Base-10 numeral system, which is the most commonly used system.

Hexadecimal: Base-16 numeral system, often used in computing.

Practice Questions on Types of Numbers:

Classify the following numbers as either prime or composite:

1. a) 17
2. b) 12
3. c) 29
4. d) 8

Answers:

1. a) 17 (Prime)
2. b) 12 (Composite)
3. c) 29 (Prime)
4. d) 8 (Composite)

Find out whether the following numbers are rational or irrational:

1. a) \sqrt{16}
2. b) 0.625
3. c) \pi
4. d) \sqrt{2}

Answers:

1. a) \sqrt{16} = 4 (Rational)
2. b) 0.625 (Rational)
3. c) \pi  (Irrational)
4. d) \sqrt{16} (Irrational)

Identify the type of number represented by each of the following:

1. a) -5
2. b) \frac{3}{4}
3. c) \sqrt{25}
4. d) 2.71828…

Answers:

1. a) -5 (Integer)
2. b) \frac{3}{4} (Rational)
3. c) \sqrt{25} = 5 (Integer)
4. d) 2.71828… (Irrational)

Classify the following numbers as either whole or natural:

1. a) -3
2. b) 0
3. c) 7
4. d) \sqrt{36}

Answers:

1. a) -3 (Neither)
2. b) 0 (Whole)
3. c) 7 (Natural)
4. d) \sqrt{36} = 6 (Natural)

Find out whether the following numbers are real or imaginary:

1. a) 4
2. b) \sqrt{-9}
3. c) 3i
4. d) -\pi

Answers:

1. a) 4 (Real)
2. b) \sqrt{-9} (Imaginary)
3. c) 3i (Imaginary)
4. d) -\pi (Real)