Table of Contents
ToggleIntroduction:
In the vast realm of calculus, few concepts are as integral and versatile as the derivative. From analyzing rates of change to optimizing functions, the derivative serves as a cornerstone for understanding dynamic systems and solving complex problems. In this detailed guide, we’ll dive into the fascinating realm of derivatives, covering what they are, how they’re calculated, their characteristics, and how they’re used in real life.
For the function y=f(x) , the derivative of the function is denoted by y' or f'(x) .
The “prime” notation y' and f'(x) was introduced by the French mathematician Joseph Louis Lagrange.
\frac{dy}{dx} or \frac{df}{dx} are standard notations for derivatives, thanks to Leibniz.
The expressions dy and dx are called “differentials”.
Definition of the Derivative (Limit Definition):
A function’s derivative tells us how the function is shifting when its input alters just a bit. The foundational definition of the derivative involves the concept of limits, specifically as the interval approaches zero. The derivative of the function f(x) with respect to x is given by,
{\color{Red} f'\left(x\right)=\lim _{h\to 0}\frac{f\left(x+h\right)-f\left(x\right)}{h} }\\
Steps to find the Derivative:
There are four steps to find the derivative of the function using the limit definition.
Step-1: For the function f(x) find f(x+h) by substituting x+h for x.
Step-2: Find the difference f(x+h)-f(x).
Step-3: Find and simplify the difference quotient \frac{f\left(x+h\right)-f\left(x\right)}{h} .
Step-4: Find the limit f'(x)=\lim _{h\to 0}\left(\frac{f\left(x+h\right)-f\left(x\right)}{h}\right) .
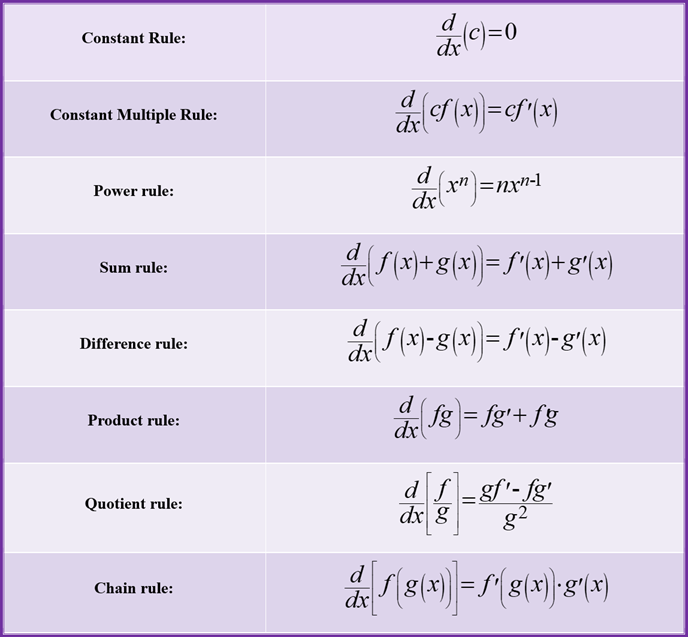
Properties of derivative:
(a) Constant Rule:
The derivative of the constant variable or constant number is always zero.
\frac{d}{dx}\left(c\right)=0
(b) Constant Multiple Rule:
When you have a constant multiplied by a function, the derivative is that constant multiplied by the derivative of the function.
\frac{d}{dx}\left(cf\left(x\right)\right)=cf'\left(x\right)\\
(c) Power rule:
For the power function x^n when n is an integer, the derivative rule is given by,
\frac{d}{dx}\left(x^n\right)=nx^{n-1}\\
(d) Sum rule:
The derivative of the sum of functions f and g is the same as adding the derivatives of f and g.
\frac{d}{dx}\left(f\left(x\right)+g\left(x\right)\right)=f'\left(x\right)+g'\left(x\right)\\
(e) Difference rule:
The derivative of the difference of functions f and g is the same as subtracting the derivatives of f and g.
\frac{d}{dx}\left(f\left(x\right)-g\left(x\right)\right)=f'\left(x\right)-g'\left(x\right)\\
(f) Product rule:
When two functions f and g are in multiplication, its derivative is given by:
\frac{d}{dx}\left(f\left(x\right)g\left(x\right)\right)=f\left(x\right)g'\left(x\right)+f'\left(x\right)g\left(x\right)\\
We can also write in simple form:
\frac{d}{dx}\left(fg\right)=fg'+f'g\\
(g) Quotient rule:
The derivative of the rational function is given by (quotient of two functions f and g):
\frac{d}{dx}\left[\frac{f\left(x\right)}{g\left(x\right)}\right]=\frac{g\left(x\right)f'\left(x\right)-f\left(x\right)g'\left(x\right)}{\left(g\left(x\right)\right)^2}\\
We can also write in simple form:
\frac{d}{dx}\left[\frac{f}{g}\right]=\frac{gf'-fg'}{g^2}\\
(h) Chain rule:
The derivative of the composite function can be calculated according to the chain rule:
For two variables: \frac{d}{dx}\left[f\left(g\left(x\right)\right)\right]=f'\left(g\left(x\right)\right)\cdot g'\left(x\right)
For three variables: \frac{d}{dx}\left[f\left(g\left(h\left(x\right)\right)\right)\right]=f'\left(g\left(h\left(x\right)\right)\right)\cdot g'\left(h\left(x\right)\right)\cdot h'\left(x\right)
Derivative of the parametric function:
To find the derivative of the parametric function, we need to use the chain rule. Let’s say you have a parametric function expressed as x(t) and y(t), where ‘t’ is the parameter. The derivative of the function y with respect to x is given by,
\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}\\
The second derivative of the parametric function:
To determine the second derivative of a parametric function, we initially compute the first derivative \frac{dy}{dx} utilizing the chain rule. Then, we proceed to differentiate it once more with respect to x.
Given parametric equations x=f(t) and y=g(t), where t is the parameter:
We can find the derivative of y with respect to x using the formula:
\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}\\
Then, to find the second derivative of y with respect to x, apply the chain rule by differentiating the first derivative \frac{dy}{dx} with respect to t and dividing by \frac{dx}{dt} .
\frac{d^2y}{dx^2}=\frac{\frac{d}{dt}\left(\frac{dy}{dx}\right)}{\frac{dx}{dt}}\\
This formula allows you to calculate the second derivative of a parametric function by first determining the first derivative with respect to the parameter and then differentiating the first derivative with respect to the parameter again. This process provides insights into the curvature and behavior of the parametric curve defined by the equations.
Derivatives Formulas:
\frac{d}{dx}\left(x\right)=1\\
\frac{d}{dx}\left(x^n\right)=nx^{n-1}\\
\frac{d}{dx}\left(cx\right)=c\\
\frac{d}{dx}\left(\ln \left(x\right)\right)=\frac{1}{x}\\
\frac{d}{dx}\left(\log _a\left(x\right)\right)=\frac{1}{x\ln \left(a\right)}\\
\frac{d}{dx}\left(e^x\right)=e^x\\
\frac{d}{dx}\left(e^{ax}\right)=ae^{ax} , Where a is any constant real number.
\frac{d}{dx}\left(a^x\right)=a^x\cdot \ln \left(a\right) , Where a is any constant real number.
Derivatives of trigonometric functions:
\frac{d}{dx}\left(\sin \left(x\right)\right)=\cos \left(x\right)\\
\frac{d}{dx}\left(\cos \left(x\right)\right)=-\sin \left(x\right)\\
\frac{d}{dx}\left(\tan \left(x\right)\right)=\sec ^2\left(x\right)\\
\frac{d}{dx}\left(\csc \left(x\right)\right)=-\csc \left(x\right)\tan \left(x\right)\\
\frac{d}{dx}\left(\sec \left(x\right)\right)=\sec \left(x\right)\tan \left(x\right)\\
\frac{d}{dx}\left(\cot \left(x\right)\right)=-\csc ^2\left(x\right)\\

When the variable x is multiplied by a then the derivatives of trigonometric functions are:
\frac{d}{dx}\left(\sin \left(ax\right)\right)=a\cos \left(ax\right)\\
\frac{d}{dx}\left(\cos \left(ax\right)\right)=-a\sin \left(ax\right)\\
\frac{d}{dx}\left(\tan \left(ax\right)\right)=a\sec ^2\left(ax\right)\\
\frac{d}{dx}\left(\csc \left(ax\right)\right)=-a\csc \left(x\right)\tan \left(ax\right)\\
\frac{d}{dx}\left(\sec \left(ax\right)\right)=a\sec \left(x\right)\tan \left(ax\right)\\
\frac{d}{dx}\left(\cot \left(ax\right)\right)=-a\csc ^2\left(ax\right)\\
Derivatives of Inverse trigonometric functions:
\frac{d}{dx}\left(\sin ^{-1}\left(x\right)\right)=\frac{1}{\sqrt{1-x^2}}\\
\frac{d}{dx}\left(\cos ^{-1}\left(x\right)\right)=-\frac{1}{\sqrt{1-x^2}}\\
\frac{d}{dx}\left(\tan ^{-1}\left(x\right)\right)=\frac{1}{1+x^2}\\
\frac{d}{dx}\left(\csc ^{-1}\left(x\right)\right)=-\frac{1}{\left|x\right|\sqrt{x^2-1}} , Where x\in \left(-\infty ,-1\right)\cup \left(-1,\infty \right)\\
\frac{d}{dx}\left(\sec ^{-1}\left(x\right)\right)=\frac{1}{\left|x\right|\sqrt{x^2-1}} , Where x\in \left(-\infty ,-1\right)\cup \left(-1,\infty \right)\\
\frac{d}{dx}\left(\cot ^{-1}\left(x\right)\right)=-\frac{1}{1+x^2}\\

When the variable x is multiplied by a then the derivatives of Inverse trigonometric functions are:
\frac{d}{dx}\left(\sin ^{-1}\left(ax\right)\right)=\frac{a}{\sqrt{1-\left(ax\right)^2}}\\
\frac{d}{dx}\left(\cos ^{-1}\left(ax\right)\right)=-\frac{a}{\sqrt{1-\left(ax\right)^2}}\\
\frac{d}{dx}\left(\tan ^{-1}\left(ax\right)\right)=\frac{a}{\left(ax\right)^2+1}\\
\frac{d}{dx}\left(\csc ^{-1}\left(ax\right)\right)=-\frac{1}{\left|x\right|\sqrt{\left(ax\right)^2-1}}, Where x\in \left(-\infty ,-1\right)\cup \left(-1,\infty \right)\\
\frac{d}{dx}\left(\sec ^{-1}\left(ax\right)\right)=\frac{1}{\left|x\right|\sqrt{\left(ax\right)^2-1}} , Where x\in \left(-\infty ,-1\right)\cup \left(-1,\infty \right)\\
\frac{d}{dx}\left(\cot ^{-1}\left(ax\right)\right)=-\frac{a}{\left(ax\right)^2+1}\\
Derivatives of hyperbolic functions:
\frac{d}{dx}\left(\sinh \left(x\right)\right)=\cosh \left(x\right)\\
\frac{d}{dx}\left(\cosh \left(x\right)\right)=\sinh \left(x\right)\\
\frac{d}{dx}\left(\tanh \left(x\right)\right)=\text{sech}^2\left(x\right)\\
\frac{d}{dx}\left(\text{csch }\left(x\right)\right)=-\text{csch }\left(x\right)\coth \left(x\right)\\
\frac{d}{dx}\left(\text{sech} \left(x\right)\right)=-\text{sech} \left(x\right)\tanh \left(x\right)\\
\frac{d}{dx}\left(\coth \left(x\right)\right)=-\text{csch }^2\left(x\right)\\
When the variable x is multiplied by a then the derivatives of Inverse trigonometric functions are:
\frac{d}{dx}\left(\sinh \left(ax\right)\right)=a\cosh \left(ax\right)\\
\frac{d}{dx}\left(\cosh \left(ax\right)\right)=a\sinh \left(ax\right)\\
\frac{d}{dx}\left(\tanh \left(ax\right)\right)=a\text{sech} ^2\left(ax\right)\\
\frac{d}{dx}\left(\text{csch }\left(ax\right)\right)=-a\text{csch }\left(x\right)\coth \left(ax\right)\\
\frac{d}{dx}\left(\text{sech} \left(ax\right)\right)=-a\text{sech} \left(x\right)\tanh \left(ax\right)\\
\frac{d}{dx}\left(\coth \left(ax\right)\right)=-a\text{csch }^2\left(ax\right)\\
Derivatives of inverse hyperbolic functions:
\frac{d}{dx}\left(\sinh ^{-1}\left(x\right)\right)=\frac{1}{\sqrt{x^2+1}}\\
\frac{d}{dx}\left(\cosh ^{-1}\left(x\right)\right)=\frac{1}{\sqrt{x^2-1}}, Where x>1\\
\frac{d}{dx}\left(\tanh ^{-1}\left(x\right)\right)=\frac{1}{1-x^2}, Where |x|<1\\
\frac{d}{dx}\left(\text{csch }^{-1}\left(x\right)\right)=-\frac{1}{\left|x\right|\sqrt{1+x^2}}, Where |x|\ne 0\\
\frac{d}{dx}\left(\text{sech} ^{-1}\left(x\right)\right)=-\frac{1}{\left|x\right|\sqrt{1-x^2}}, Where 0<x<1\\
\frac{d}{dx}\left(\coth ^{-1}\left(x\right)\right)=\frac{1}{1-x^2}, Where |x|>1\\

When the variable x is multiplied by a then the derivatives of Inverse hyperbolic functions are:
\frac{d}{dx}\left(\sinh ^{-1}\left(ax\right)\right)=\frac{a}{\sqrt{\left(ax\right)^2+1}}\\
\frac{d}{dx}\left(\cosh ^{-1}\left(ax\right)\right)=\frac{a}{\sqrt{\left(ax\right)^2-1}}, Where x>1\\
\frac{d}{dx}\left(\tanh ^{-1}\left(ax\right)\right)=\frac{a}{1-(ax)^2}, Where |x|<1\\
\frac{d}{dx}\left(\text{csch }^{-1}\left(ax\right)\right)=-\frac{1}{x\sqrt{1+\left(ax\right)^2}}, Where |x|\ne 0\\
\frac{d}{dx}\left(\text{sech} ^{-1}\left(ax\right)\right)=-\frac{1}{\left|x\right|\sqrt{1-(ax)^2}}, Where 0<x<1\\
\frac{d}{dx}\left(\coth ^{-1}\left(ax\right)\right)=\frac{a}{1-(ax)^2}, Where |x|>1\\
Types of Derivatives:
(a) First Order Derivative:
The first-order derivative, also known as the first derivative or simply the derivative, represents the rate of change of a function with respect to its independent variable.
The first-order derivative f'(x) also represents the slope of the tangent line to the graph of f(x) at a given point x.
The first-order derivative f(x) is calculated using the limit definition of the derivative:
f'\left(x\right)=\lim _{h\to 0}\frac{f\left(x+h\right)-f\left(x\right)}{h}\\
This limit represents the rate of change of f(x) as h approaches zero. Geometrically, it corresponds to the slope of the tangent line to the graph of y=f(x) at the point (x,y).
It indicates the rate at which a function is changing compared to its independent variable x.
The first-order derivative provides valuable information about the behavior of a function, including its increasing and decreasing intervals and, critical points.
If f'(x)>0, the function is increasing.
If f'(x)<0, the function is decreasing
If f'(x)=0, the function has a critical (extreme) point at point x.
(b) Second Order Derivative:
It indicates the curvature of the graph of the function at a given point x.
The second-order derivative can be obtained by taking the derivative of the first-order derivative:
f''\left(x\right)=\frac{d}{dx}\left(f'\left(x\right)\right)\\
The second-order derivative provides information about the concavity of the function.
If f”(x)>0, the function is concave upward. (The curve is bending upwards.)
If f”(x)<0, the function is concave downward. (The curve is bending downward.)
If f”(x)=0, the function has an inflection point at point x.
(c) Higher Order Derivatives:
Higher order derivatives refer to derivatives of functions that are taken beyond the first and second derivatives. In calculus, functions can be differentiated multiple times to obtain higher-order derivatives, which provide information about the rates of change of rates of change, curvature, and other properties of the function.
For a function f(x), the n-th order derivative, denoted by f^{(n)}(x) or \frac{d^n}{dx^n}\left(f\left(x\right)\right), represents the n-th derivative of the function with respect to the independent variable x. They can be used to study the Taylor series expansions and solve differential equations.
(d) Implicit Differentiation:
Implicit differentiation is a method used to find the derivative of a function.
This method proves beneficial when dealing with equations that are not easy to solve directly for the dependent variable.
Let’s consider one example.
x^2+y^2=4\\
Differentiate both sides with respect to x.
\frac{d}{dx}\left(x^2+y^2\right)=\frac{d}{dx}\left(4\right)\\
\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(y^2\right)=0\\
2x+2y\cdot \frac{dy}{dx}=0\\
2y\cdot \frac{dy}{dx}=-2x\\
\frac{dy}{dx}=-\frac{2x}{2y}\\
\frac{dy}{dx}=-\frac{x}{y}\\


